Problem set link.
The key observation is that the two closest students will be in sequential order if we sort the array. So our solution first sorts the array, and then checks all consecutive pairs of elements for the minimum.
import java.util.Arrays;
import java.util.Scanner;
public class ExamRoom {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] positions = new int[n];
for (int i = 0; i < n; i++) {
positions[i] = sc.nextInt();
}
Arrays.sort(positions);
int minDistance = Integer.MAX_VALUE;
// Iterate through the sorted array and find the minimum difference
for (int i = 1; i < n; i++) {
int diff = positions[i] - positions[i - 1];
if (diff < minDistance) {
minDistance = diff;
}
}
System.out.println(minDistance);
}
}
This problem is about computing something known as the number of inversions of an array: the number of pairs $i, j$ such that $i < j$ but $p_i > p_j$. (Note that this exactly corresponds to the number of comparisons made by a insertion sort algorithm). Computing this directly looks hard (at least if you want to do it in time better than $O(n^2)$). But there is a way of solving this problem based on modifying merge sort. if you don’t know how, think about it for a bit, and then read the rest of this description.
Let’s first solve the following simplified problem: suppose you have an array that is made of two sorted arrays (but the concatenation of the two might not be sorted), what is the inversions of this array? We can slightly modify the merge operation of merge sort, and merge the two concatenated sorted arrays. Recall that in the merge operation we repeatedly compare the first element of each of the arrays and move the smallest of the two to a new array. Suppose the next smallest element is the first of the second array (and so we move it to the new array). So this element is smaller than all current elements in the left array, which means each element currently in the left array induces one inversion. So we can update our count of inversions!
To generalize this to solve the full problem, note that all we need to do is run merge sort with this modified merge that counts inversions and keep track of the total number of inversions.
Here is a short solution based on the merge sort from
COS226. Note
how simple and similar to merge sort it is (the difference is only
about 4 extra lines of code). Also, note we used a long instead of a
int to count the inversions, to avoid overflow.
import java.util.Scanner;
public class PizzaLine {
static long sortAndCount(int[] a, int[] aux, int lo, int hi) {
if (hi <= lo) return 0;
int mid = lo + (hi - lo) / 2;
long count = 0;
count += sortAndCount(a, aux, lo, mid);
count += sortAndCount(a, aux, mid+1, hi);
count += mergeAndCount(a, aux, lo, mid, hi);
return count;
}
static long mergeAndCount(int[] a, int[] aux, int lo, int mid, int hi) {
for (int k = lo; k <= hi; k++)
aux[k] = a[k];
long count = 0;
int i = lo, j = mid+1;
for (int k = lo; k <= hi; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > hi) a[k] = aux[i++];
else if (aux[j] < aux[i]) {
a[k] = aux[j++];
count += (mid + 1 - i);
}
else a[k] = aux[i++];
}
return count;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] p = new int[n];
for (int i = 0; i < n; i++) {
p[i] = sc.nextInt();
}
int[] aux = new int[n];
long unhappiness = sortAndCount(p, aux, 0, n - 1);
System.out.println(unhappiness);
}
}
We need to use the technique of sweep line to solve this efficiently. The intuition of the idea is the following, we draw all the intervals on a line and imagine a line sweeping through the intervals from left to right, keeping track of when the line is intersecting some interval.
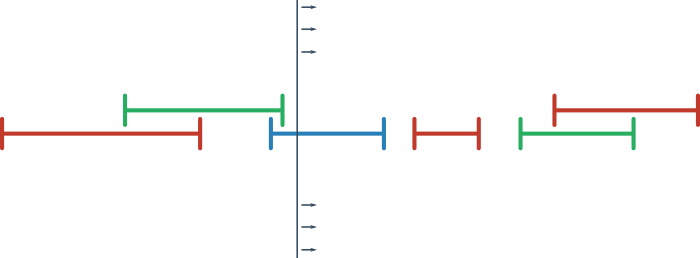
To turn this into an algorithm, let’s first sort all the intervals by
start point and tiebreak based on end point. Now let’s iterate through
each interval by this order (which is corresponds to sweeping through
the intervals). To process the first interval, let’s keep track of the
start point of this interval, since it will be the very first start
point of any interval. Let’s also keep track of the end point of this
interval, since this is the furthest end point we’ve seen so far, in a
variable called endSoFar. When we move to the next interval, two
things can happen:
endSoFar. In
this situation we update endSoFar to be the maximum between its
current value and the end point of the new interval, in case this
new interval pushes the boundary of the current interval further to
the right.import java.util.Arrays;
import java.util.Scanner;
private class Interval implements Comparable<Interval> {
int start, end;
Interval(int start, int end) {
this.start = start;
this.end = end;
}
public int compareTo(Interval other) {
if (this.start != other.start) return this.start - other.start;
else return this.end - other.end;
}
}
public class ClassSchedule {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
Interval[] intervals = new Interval[n];
for (int i = 0; i < n; i++) {
int start = sc.nextInt();
int end = sc.nextInt();
intervals[i] = new Interval(start, end);
}
Arrays.sort(intervals);
// Sweep line!
int totalHours = 0;
int startSoFar = intervals[0].start;
int endSoFar = intervals[0].end;
for (int i = 1; i < n; i++) {
if (intervals[i].start <= endSoFar) {
// Overlapping intervals, merge them
endSoFar = Math.max(endSoFar, intervals[i].end);
} else {
// Non-overlapping, accumulate the time
totalHours += endSoFar - start;
// New interval starts
start = intervals[i].start;
endSoFar = intervals[i].end;
}
}
// Add the last interval
totalHours += endSoFar - start;
System.out.println(totalHours);
}
}
This is the first problem where we don’t have to sort anything, but the solution is actually based on the same idea that makes quicksort work.
First, observe that you can always paint the whole fence with $n$
vertical strokes. Now, consider the lowest plank in the fence, and
suppose it is of height $x$. Any solution that doesn’t use all
vertical strokes will have to use at least $x$ horizontal strokes,
since if you are going to use horizontal strokes, you might as well
cover the shortest planks first. If you add $x$ horizontal strokes,
now you can basically remove $x$ from the fence and it is now split
into a few “subfences” (potentially of different sizes). How do we
handle these subfences? Well, recursively. If we implement a function
that counts the minimum number of strokes, it either returns the
length of the fence (corresponding to all vertical strokes) or it adds
$x$ vertical strokes and now it calls itself on each of the subfences
formed by removing the planks of height $x$. Note that in this
recursive call we have to assume that we’ve painted the bottom $x$
meters of the planks (we can either update the heights array by
subtracting $x$ from its elements, or use a variable coveredSoFar
that keeps track of how much we have painted from the bottom up
horizontally).
import java.util.Scanner;
public class PaintingFence {
public static int minStrokes(int[] heights, int l, int r, int coveredSoFar) {
if (l > r) return 0;
int minHeight = Integer.MAX_VALUE;
for (int i = l; i <= r; i++) {
minHeight = Math.min(minHeight, heights[i]);
}
int strokes = minHeight - coveredSoFar;
int prevMin = l;
for (int i = l; i <= r; i++) {
if (heights[i] == minHeight) {
strokes += minStrokes(heights, prevMin, i - 1, minHeight);
prevMin = i + 1;
}
}
// The above for loop doesn't consider the very last block
strokes += minStrokes(heights, prevMin, r, minHeight);
return Math.min(strokes, r - l + 1);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] heights = new int[n];
for (int i = 0; i < n; i++) {
heights[i] = sc.nextInt();
}
System.out.println(minStrokes(heights, 0, n - 1, 0));
}
}
See the solutions of the Compete Division for the solution to this problem.